"In medias res"
A prÃmszámok vizsgálata során, arra a következtetésre jutottam, miszerint a prÃmszámok elÅ‘fordulása, teljes mértékben egy logikus képletet követve történik. Elméletem jelenleg csak a prÃmszámok logikáját magyarázza.
Tételezzük fel, hogy a számok a koordináta rendszerben hullámszerűen terjednek. Minden egyes adott szám egy akkora sinus hullámot indÃt el, amely a nullától való távolsága. Ezek után tételezzük fel, hogy az egy , kettÅ‘ , három alapszámok és az elsÅ‘ duplázó hullám után következik az elsÅ‘ prÃmszám. Tény, hogy az alapszámok és a prÃmszámok kapcsolata végig megmarad. Ebben az esetben a kettes és a hármas szám elindÃt egy sinus (1/2x) és egy sinus ( 1/3x) hullámot. (1.ábra ). Ezen hullámok üres tartományaiban (zérus helyek) megkapjuk az elsÅ‘ prÃmszámokat (p1=5) és azok többszöröseit. A zérus értékek(Pn) szintén elÃndÃtanak egy sin(x) hullámot és Ãgy kiesnek a prÃmszámok értékeinek szorzatai. Ezek a kiesÅ‘ prÃmszámok szintén a 6n+/- 1 értékeken találhatóak.
1.ábra
A prÃmszámok logikája
A 6 többszörösei +-1 függvény alakÃtja ki a prÃmszámok és a prÃmszámok többszöröseinek függvényét. A prÃmszámok 6n+/-1 függvénye az elsÅ‘ prÃmszám, azaz a p1 érték négyzeténél szakad meg és innen egy metodus szerint szűri ki a prÃmszámok többszöröseit illetve a prÃmszámok szorzatait. A szűrÅ‘ ( 2. ábra ) az elsÅ‘ prÃmszámtól indulva váltakozva 7p és 3p távolságonként szűri meg a tényleges prÃmszámokat. A következÅ‘ prÃmszám szűrÅ‘je váltakozva 9p és 5p távolságonként. A következÅ‘ azaz harmadik prÃmszám 15p és 7p távolságban szűri a prÃmszámokat. Tehát az elsÅ‘ prÃmszámtól kezdve váltakozva, minden következÅ‘ prÃmszám +2/+2 és +6/+2 p szerint szűri ki a prÃmszámok szorzatait és többszöröseit. (pnv). Az alábbi képek segÃtenek megérteni a hullámelmélet működését.
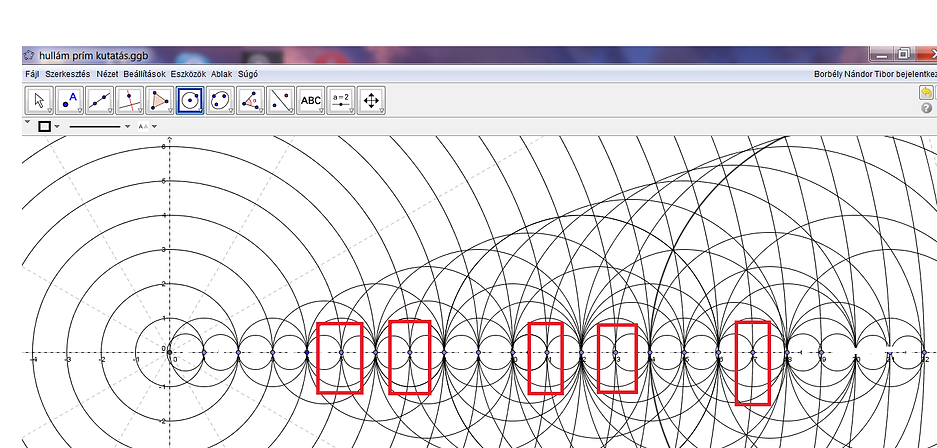
2.ábra
A kettes és a hármas hullámok
A kettes, hármas , ötös hullámok
PrÃmszámok hullám elmélete
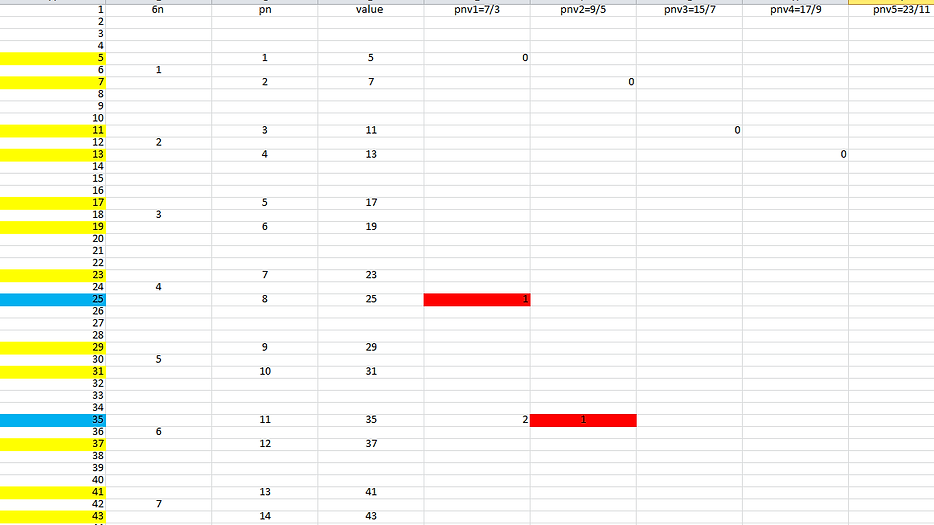
Hullámelmélet táblázatban
